Compilers

Ch1

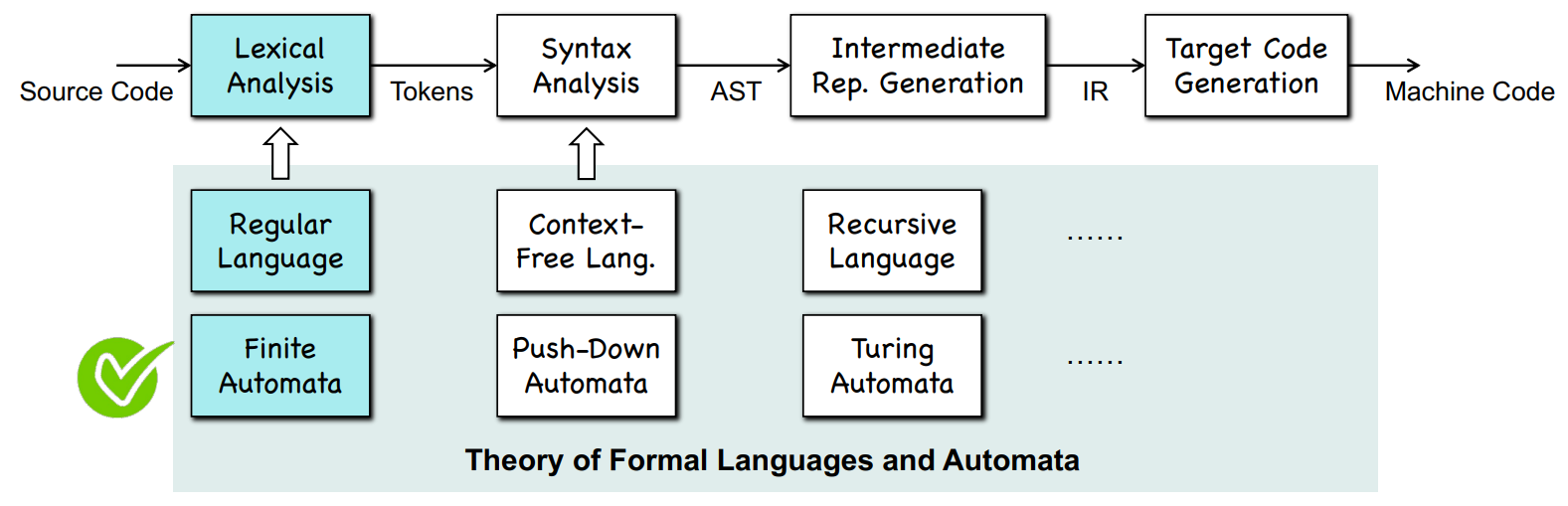
Front End

Lexical Analysis -> Syntax Analysis -> Semantic Analysis

Lexical Analysis (词法分析)

  • Create tokens

    <token-class, attribute>

Syntax Analysis (语法分析)

  • Create the abstract syntax tree (AST)

Semantic Analysis (语义分析)

  • Check the correct meaning
  • Decorate the AST

IR Generation:

  • Generate machine-independent intermediate representation (IR) based on the syntax tree

Middle End

Optimizations

Back End

Instruction Selection

  • Translate IR to machine code
  • Perform machine-development optimization

Register Allocation

Instruction Scheduling

  • (for example: parallelism)

Ch3

Ch3-1 Finite Automata

Empty String: ϵ

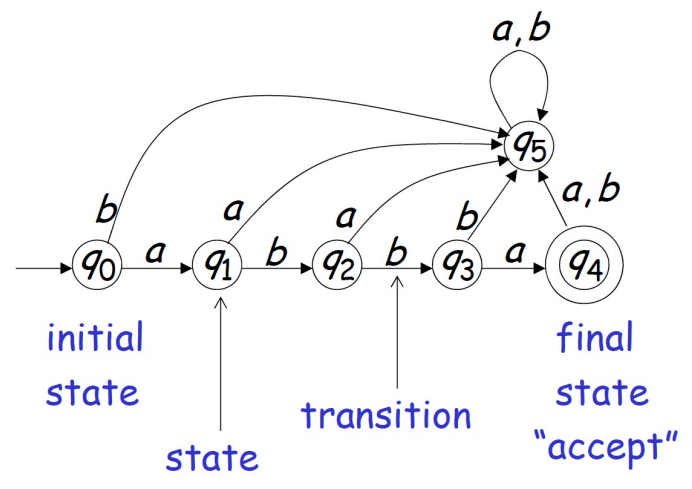
Deterministic Finite Automata

A DFA is formally defined as a 5-tuple (Q, Σ, δ, q₀, F), where:

  • Q: A finite set of states.
  • Σ: A finite input alphabet.
  • δ: A transition function δ: Q × Σ → Q that maps a state and an input symbol to a single next state.
  • q₀: The start state, where the DFA begins processing.
  • F: A set of accept states, F ⊆ Q.
DFA Minimization
DFA Bi-Simulation

Non-deterministic Finite Autometa

Allow ϵ-transitions.

ϵ-Closure

ϵ-closure(q) returns all states q can reach via ϵ-transitions, including q itself.

From NFA to DFA

ϵ-Closure

  • When converting an NFA to a DFA, there is no guarantee that we will have a smaller DFA.

Ch3-2 Lexical Analysis

Laws of Regex

  • Commutativity and Associativity
  • Identities and Annihilators
  • Distributive and Idempotent Law
  • Closure

Regex = Regular Language

  • Any regex represents a regular language NFA/DFA
  • Any regular language DFA can be expressed by a regex

Lexical Analysis

symbol table

Pumping Lemma

If L is an infinite regular language (the set L is infinite),

there must exist an integer m,

for any string w ∈ L with length |w| ≥ m,

we can write w = xyz with |xy| ≤ m and |y| ≥ 1,

such that wi = xyiz ∈ L

Ch4-1

Context-Free Language

Context Free Grammar (CFG)

A context-free grammar is a tuple G = (V, T, S, P)

  • V: a finite set of non-terminals
  • T: a finite set of terminals, such that V ∩ T = ∅
  • S ∈ V: start non-terminals

Regular language ⊆ Context-free language

Context-free language = Push-down automata

Left-Most Derivation (=>lm)

In every step derivation, we replace the left-most non-terminal.

Right-Most Derivation (=>rm)

In every step derivation, we replace the right-most non-terminal.

Parse/Syntax Trees

Parse tree

  • Every leaf is a terminal
  • Every non-leaf node is a non-terminal

Ambiguity

A grammar is ambiguous if there is a string has two different derivation trees.

Eliminating Ambiguity

Lifting operators with higher priority

Using Ambiguous Grammar

Push-Down Automata (PDA)

NPDA

Context-free language = PDA = NFA + Stack = NPDA (Non-Deterministic PDA)

NPDA/PDA is defined by the septuple:

  • Q = (Q, Σ, Γ, δ, q0, z0, F)
  • Q: a finite set of states
  • Σ: finite input alphabet
  • Γ: finite stack alphabet
  • δ: Q × (Σ ∪ {ϵ})×Γ ⟼ 2Q× Γ*: transition
  • q0 ∈ Q: initial state
  • z0 ∈ Γ: stack start symbol
  • F ⊆ Q: set of final states

Instantaneous Description

An instantaneous description of a PDA is a triple

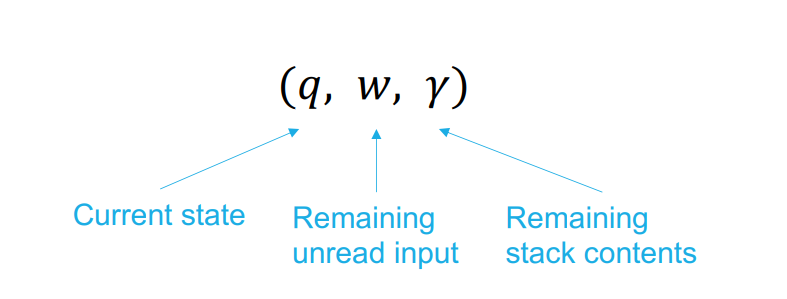
Language of PDA

At the end of computation, we don’t care about stack contents

acceptance by final states:

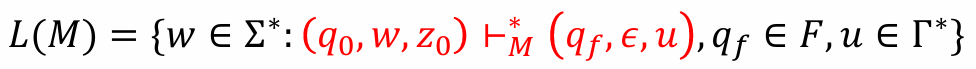
acceptance by empty stack:

Equivalence of PDA and CFG

TBD

Properties of CFL

Closure Properties

Given two CFL, L1 and L2, the following are CFL

  • L1 ∪ L2
  • L1L2
  • L1*
  • L1R（ = \(\{w^R:w \in L_1 \}\)）

Given two CFL, L1 and L2, the following may not be CFL

  • L1 ∩ L2（ = \(\overline{\overline{L_1} \cup \overline{L_2} }\)）
  • \(\overline{\textit{L}}\)1
  • L1 - L2

Pumping Lemma for CFL

Chomsky Normal Form

\(A \rightarrow BC;\)

\(A \rightarrow \alpha;\)

\(S\rightarrow\epsilon;\)

Pumping Lemma for CFL

Given a CFL \(L\), there exists a constant \(n\) such that we have \(z=uvwxy \in L,\ |z| \geq n\) satisfying the condition below

  • \(vx\neq\epsilon\)
  • \(|vwx|\leq n\)
  • \(\forall i \geq 0,\ z_i=uv^iwx^iy\in L\)

Ch4-2

Top-Down Parsing

Constructing a parse tree in preorder.

  1. Backtracking may be necessary.
  2. A left-recursive grammar can cause infinite loops.

Eliminating Left-Recursion

\(A\rightarrow A\alpha\ |\ \beta\) can be transformed into:

\(A\rightarrow \beta A^{'}\)

\(A^{'}\rightarrow\alpha A^{'}\ | \ \epsilon\)

Predictive Parsing

Predictive parsers are recursive descent parser without backtracking.

LL(1)

  • L: scanning input from left to right
  • L: leftmost derivation
  • 1: Using one input symbol of lookahead at each step

FIRST()

\(FIRST(\alpha)\): A set of terminals that 𝛼 may start with.

  • If \(X\) is a terinal, FIRST(\(X\)) ={\(X\)}

  • If \(X\rightarrow \epsilon\) is a production, \(\epsilon \in\) FIRST(\(X\))

  • If \(X \rightarrow Y_1Y_2...Y_k,\)

    \(\epsilon \in \cap_{j=1}^{i-1}FIRST(Y_j) \land a \in FIRST(Y_i) \Rightarrow a \in FIRST(X)\)

    \(\epsilon \in \cap_{j=1}^{i-1}FIRST(Y_j) \Rightarrow \epsilon \in FIRST(X)\)

FOLLOW()

\(FOLLOW(\alpha)\): A set of terminals that can appear immediately to the right of \(\alpha\)

  • \(\$ \in FOLLOW(S)\), where \(\$\) is string's end marker, \(S\) the start non-terminal
  • \(A \rightarrow \alpha B\beta \Rightarrow FIRST(\beta)\backslash\{\epsilon\} \subseteq FOLLOW(B)\)
  • \(A\rightarrow \alpha B\ or\ A \rightarrow \alpha B\beta \ where\ \epsilon \in FIRST(\beta)\Rightarrow FOLLOW(A)\subseteq FOLLOW(B)\)

Predictive Parsing Table

To build a parsing table \(M[A,a]\), for each \(A\rightarrow \alpha\)

  • \(\forall a \in FIRST(\alpha):\ M[A,a] = A \rightarrow \alpha\)
  • \(\epsilon \in FIRST(\alpha) \Rightarrow \forall b \in FOLLOW(A):\ M[A,b]=A \rightarrow \alpha\)

LL(1) Grammar: Formal Definition

A grammar is LL(1) if and only if any \(A \rightarrow \alpha\ |\ \beta\) satisfies:

  • For no terminal \(\alpha\) do both \(\alpha\) and \(\beta\) derive strings starting with \(a\) (by left factoring)
  • At most one of \(\alpha\) and \(\beta\) derive the empty string
  • if $^* $, \(\alpha\) doesn't derive strings starting with terminals in FOLLOW(\(\alpha\))

Bottom-Up Parsing

Constructing a parse tree in post-order.

  • Keep shifting until we see the right-hand side of a rule.
  • Keep reducing as long as the tail of our shifted sequence matches the right-hand side of a rule. Then go back to shifting.

LR(0)

We don't need to make decisions during parsing.

  • Left-to-right scanning
  • Right-most derivation
  • Zero symbols of lookahead

Ch6-1

Intermediate Representation

Three Address Code

  • Provide a standard reputation
  • At most one operator on the right side of each instruction
  • At most three addresses/variables in an instruction

Generation of Three-Address Code

Syntax-Directed Definition (SDD)

SDD = Context-Free Grammar + Attributes + Rules

Ch6-2

SSA and Extensions

Static Single-Assighment

  1. Every variable has only one definition.

    Direct def-use chains

  2. Using \(\phi\) to merge definitions from multi paths.

    1
    2
    3
    4
    5
    6
    7
    8
    if(flag) x = -1;
    else x = 1;
    y = x * a;
    =>
    if(flag) x1 = -1;
    else x2 = 1;
    x3 = \phi(x1, x2);
    y = x3 * a;
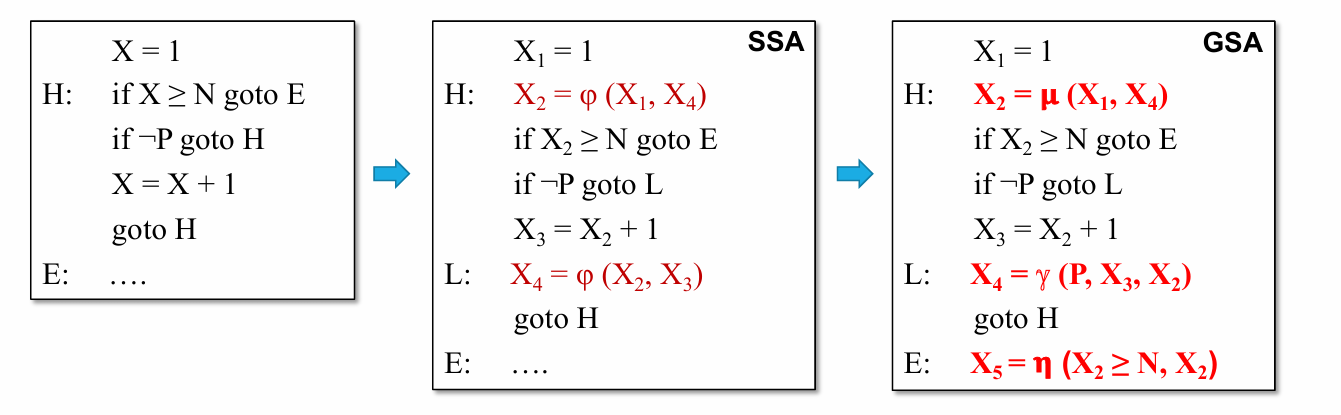
Gated SSA (GSA)

  1. Every variable has only one definition.

  2. Use recursive \(\gamma\) to merge definitions from multi-paths.

    Direct def-use chains + conditional def-use chains

    1
    2
    3
    4
    5
    6
    if(flag) x = -1; else x = 1;
    y = x * a;
    =>
    if(flag) x1 = -1; else x2 = 1;
    x3 = \gamma(flag, x1, x2);
    y = x3 * a;

  3. use \(\mu\) and \(\eta\) for loop variables.

SSA Complexity

Space & Time: Almost linear

LLVM IR

Translation into SSA

Basic Block

A sequence of consecutive instructions.

The first instruction of each block is a leader.

Loop

Dominance & Post-Dominance

  • A dom B
    • if all paths from Entry to B goes through A
  • A post-dom B
    • if all paths from B to Exit goes through A
  • Strict (post-)dominance - A (post-)dom B but A \(\neq\) B
  • immediate dominance - A strict-dom B, but there's no C, such that A strict-dom C, C strict-dom B

Dominator Tree

Almost linear time to build.

  • Node: Block
  • Edge: Immediate dom relation

(Nearest) common dominator

  • LCA - lowest common ancestor

Dominance vs. Ctrl Dependence

Block B is control dependent on Block A

if and only if

  • the execution result of A determines if B will be executed.

<=>

  1. A has multiple successors
  2. Not all successors can reach B

<=>

  1. B post-dominates a successor of A
  2. B does not post-dominates all successors of A

Dominance Frontier

DF(A) = {...}

  • The immediate successors of the blocks dominated by A
  • Not strictly dominated by A (A itself)

Iterated Dominance Frontier

\(DF(Bset) = \cup_{B\in Bset}DF(B)\)

Iterated DF of Bset:

  • DF1 = DF(Bset); Bset = Bset ∪ DF1
  • DF2 = DF(Bset); Bset = Bset ∪ DF2
  • ……
  • until fixed point!

IDF vs. SSA

Ch8-1

Targret Code Generation

  • Memory (Heap/Stack/...). Each byte has an address.
  • n Registers: R0, R1, ..., Rn-1. Each for bytes.
  • Load/Store/Calculation/Jump/...(Like x86 assembly)

In-Block Optimization

Peephole Optimization

Ch8-2

The Lost Copy Problem

The Swap Problem

Ch 8-3

Register Allocation

Pysical machines have limited number of registers.

Register allocation: \(\infty\) virtual registers \(\rightarrow\) \(k\) physical registers

Local Register Allocation

Requirement:

  • Produce correct code using \(k\) or fewer registers
  • Minimize loads, stores, and space to hold spilled values
  • Efficient register allocation (\(O(n)\) or \(O(n\log{n})\))

Spilling:

  • saves a value from a register to memory
  • the register is then free for other values
  • we can load the spilled value from memory to register when necessary

MAXLIVE: the maximum of values live at each instruction

  • MAXLIVE ≤ k ---Allocation is trivial
  • MAXLIVE > k--- Values must be spilled to the memory

Global Register Allocation

Global allocation often uses the graph-coloring paradigm

  • Build a conflict/interference graph
  • Find a k-coloring for the graph, or change the code to a nearby problem that it can color
  • NP-complete under nearly all assumptions, so heuristics are needed

K-Coloring